Density Plots: Examples, Types, Best Practices, and How to Build One

Simple averages often miss key patterns in your data. But density plots can reveal hidden distributions, showing where values are clustered, spread, or concentrated to provide a clearer picture of your data’s structure.

Knowing how your data is distributed uncovers valuable information that averages alone can’t provide. With density plots, you can see where your data clusters or spreads, spot outliers, and really dig into the underlying patterns. This makes them an essential tool for exploring and understanding your data. 

In this guide, we’ll cover core definitions, share possible use cases, give some design tips, walk through different examples, and provide step-by-step instructions for creating density plots.

What is a density plot?

A density plot visualizes the distribution of a continuous variable by drawing a smooth curve rather than using bars, like you might find in a smoothed histogram. But unlike histograms, which group data into bins and represent counts as bars, density plots estimate the concentration of values across the range. This smooth representation reveals the underlying shape of the data, highlighting peaks and skewness without being influenced by bin choices.

The smooth curve in a density plot is created by applying kernel density estimation. This method overlays a bell-shaped curve, or “kernel,” on each data point, then adds all the kernels together. Areas where kernels overlap form peaks, highlighting where values are most heavily concentrated.

When to use a density plot (and why) 

Density plots work best for showing the distribution of continuous data. They help you compare how values are spread across categories and highlight features like skewness, peaks, or gaps. Use them when you want to identify clusters, detect multiple modes, or observe subtle shifts in distributions that histograms might obscure. 

Choose a density plot when you want to understand the shape and concentration of data in detail, especially when comparing multiple groups.

Best use cases for density plots

• Analyzing distributions of continuous data
  This is their primary function. If you have a column of numerical data like temperatures, sales amounts, user ages, or test scores, a density plot provides an intuitive look at how those values are spread out. You can instantly see if the data is symmetric, skewed, or has multiple peaks.
• Comparing multiple distributions
  Density plots are particularly powerful for comparing the distributions of a variable across different categories. For example, you could compare the distribution of customer purchase amounts for different regions or the distribution of test scores between two groups of students. Overlapping the density curves on a single chart makes these comparisons direct and clear.
• Identifying skewness, peaks, or outliers
  The smooth line of a density plot makes it easy to spot key characteristics. A peak (or mode) indicates where the data is most concentrated. A distribution with one peak is unimodal, while one with two is bimodal. Skewness, or a lack of symmetry, is also easy to see. If the tail of the plot extends further to the right, the data is right skewed. If it extends to the left, it’s left skewed. Density plots aren’t designed for detecting outliers; however, having long, thin tails on a plot can suggest extreme values in the data.

Advantages of using density plots

The main advantage of density plots is their ability to smoothly show the shape of your data. They avoid the problems of bin choice in histograms, offering a clearer and more consistent view of the underlying distribution.

Density plots also make comparisons between distributions much easier and clearer. While overlaying multiple histograms can result in a cluttered, hard-to-read chart, density plots allow you to display several semi-transparent curves on a single axis. This setup makes it easy to compare shapes, peaks, and spreads, while highlighting the differences and similarities across your data.

When not to use a density plot

Density plots aren’t suitable for very small data sets or for categorical and discrete data.

• Very small data sets: Kernel density estimation works best with a reasonably large number of data points. With a very small data set, the resulting plot can be noisy and misleading, as the estimation algorithm has less information to work with. In these cases, a strip plot or a simple histogram might be more honest about the data you have.
• Categorical or discrete data: Density plots are designed exclusively for continuous data. Using them for categorical variables (like “red,” “blue,” “green”) or discrete numerical data with only a few possible values (like the number of cars a family owns) doesn’t make sense and will produce a meaningless chart. For such data, bar charts are the appropriate tool.

How density plots work: The mechanics

Density plots are created using kernel density estimation (KDE). This technique works by placing a small, smooth, bell-shaped curve (called a “kernel”) over each data point, then adding these curves together. Where kernels overlap, you see peaks; where few overlap, you get valleys. This creates the density plot’s smooth, continuous curve that highlights areas of concentration in your data.

The key control in this process is the bandwidth, which controls how smooth or detailed your density plot appears: a narrow bandwidth produces a jagged curve, while a wide one creates a smoother plot that may hide important details.

The role of bandwidth and smoothing

Choosing the bandwidth is crucial: too narrow, and the plot looks noisy; too wide, and important features can disappear. The right bandwidth balances clarity and detail so the plot accurately represents your data’s structure.

• Small bandwidth (“under-smoothing”): Each kernel is very narrow, so the resulting plot will be highly detailed and “bumpy,” closely following the individual data points. This can be useful for spotting fine-grained structure, but it can also create a noisy plot that’s hard to read. It might show bumps and wiggles that are just random noise rather than true features of the distribution. 
• Large bandwidth (“over-smoothing”): Each kernel is very wide, so the resulting plot will be very smooth, glossing over the finer details. This can make it easier to see the major, overarching shape of the distribution, but it risks hiding important features like smaller peaks. 

Choosing an appropriate bandwidth is essential. It controls the smoothness of the density plot, helping reveal your data’s true structure without losing important patterns or introducing excess noise. Experiment with this setting to make sure your plot accurately represents your data.

Understanding density plot axes

Understanding how to read density plot axes is essential.

• X-axis: This axis displays the range of values for your continuous variable, such as age, income, or response time. This axis is straightforward. It represents the values of the continuous variable you are plotting. If you are plotting customer ages, the x-axis will show age.
• Y-axis: This axis shows probability density, not a count or frequency. This means you can’t interpret the height of the curve as the number of data points at a specific value. Instead, the important aspect is the area under the curve: the region between any two points on the x-axis represents the proportion of data values (probability) that fall within that range. The total area under the curve is always equal to 1, which represents the entire data set (100 percent probability).

Focus on comparing the relative heights of the curves, as higher curves mean a greater concentration of data. When comparing multiple density plots, be sure they share the same y-axis scale for a fair comparison of relative densities. Since the y-axis shows the relative concentration of data values across the range, it highlights where values cluster, rather than providing exact counts. So always use a consistent y-axis scale for meaningful comparisons.

Types and variants of density plots

There are several main types of density plots, each serving different analysis needs. You can use a single density plot for one continuous variable, overlay multiple density plots to compare groups, stack density plots to see several distributions together, or choose between filled and line-based styles depending on clarity and design. Selecting the right type helps you clearly communicate your data’s story.

Single density plot

A single density plot shows the distribution of one continuous variable as a smooth curve, offering a clear view of where values are concentrated in a data set. Use it for a quick overview of data spread and central tendencies.

Multiple overlapping density plots

Multiple overlapping density plots show how a variable’s distribution differs across groups by layering their curves on the same chart. This lets you compare group patterns directly and spot similarities or differences at a glance.

Overlapping density plots make it easy to compare patterns between groups. Using distinct colors and transparency helps you spot differences and similarities in peaks, spread, and shape. This design highlights group comparisons while keeping the chart readable.

Stacked density plots

A stacked density plot, also called a ridgeline plot, arranges multiple density curves in vertical layers. Each layer shows a category, making it easy to compare several distributions without the clutter of overlapping lines.

Stacked density plots are ideal for comparing many distributions at once without clutter. By arranging each curve in its own layer, you can quickly spot patterns, shifts, or differences across multiple groups in a compact and readable format.

Filled vs line-based density plots

Density plots come in two main styles: line-based and filled. Line-based density plots display only the outline of the curve, while filled density plots color the area under the curve.

• Line-based plots are clean and are generally the best choice when overlapping multiple distributions, as they minimize visual clutter.
• Filled plots, where the area under the curve is colored in, can be visually striking, especially for a single distribution. When using filled plots for multiple overlapping distributions, transparency is absolutely essential so that curves in the background aren’t completely obscured.

Choose filled plots for single distributions when you want a bold visual and opt for line-based plots when comparing multiple distributions to keep the chart clear and easy to read.

Design best practices and pitfalls

Designing an effective density plot requires careful choices to keep your chart clear and accurate. Follow these key best practices and avoid common mistakes for the best results.

Choose bandwidth carefully

Bandwidth sets the smoothness of a density plot. If it’s too wide, the plot becomes overly smoothed and important details disappear. If it’s too narrow, the plot looks jagged and random noise appears as false features. Choosing the right bandwidth keeps your plot both clear and insightful.

• Avoid over-smoothing: This happens when the bandwidth is too large. Your plot will look like a simple, wide hill, masking important features like bimodality (two peaks). You might mistakenly conclude your data is simple when it actually has a complex structure.
• Avoid-under smoothing: This occurs when the bandwidth is too small. Your plot will appear jagged and noisy, with many small bumps that are likely just random fluctuations in your sample data, not real features of the underlying population.

Most software provides a default bandwidth, but it’s essential to try different values. Adjusting the bandwidth helps you balance smoothness and detail, ensuring your density plot accurately reflects your data without hiding patterns or adding noise.

Use transparency when overlapping densities

When comparing multiple distributions on the same plot, use semi transparent colors so overlapping areas remain visible. This makes it easier to see how the distributions relate, overlap, and differ. An opacity level of 30 percent to 60 percent is usually effective.

Limit the number of distributions

Too many overlapping distributions can make a plot confusing. Limit overlays to three or four groups for clarity.

If you’re trying to compare more than four distributions, switch to a stacked density plot (also called a ridgeline plot). By placing each distribution on its own horizontal line, you’ll avoid overlap and make comparisons clear and simple. 

Alternatively, use small multiples: create a grid of separate density plots where each group is shown in its own subplot. Both approaches keep your visualization organized and allow easy comparison across categories without the confusion of overlapping too many curves.

Label clearly to avoid confusion

Clear labeling is essential in density plots. Well-labeled charts prevent confusion, guide interpretation, and guide your audience to the insights your data provides.

• Title: Give your plot a clear, descriptive title that explains what it shows. For example, “Distribution of Customer Purchase Amounts by Membership Tier.”
• Axis labels: Clearly label the x-axis with the variable name and its units (e.g., “Age in Years”). For the y-axis, simply labeling it “Density” is standard practice. While the absolute values aren’t intuitive, the label clarifies that it’s not a count.
• Legend: If you are plotting multiple distributions, include a clear legend that identifies which color corresponds to which category.

Avoid misleading y-axis interpretations

A common mistake is to misread the y-axis, which shows probability density, not the number of data points or their frequency. The height of the curve reflects how concentrated the data is at specific values, but not actual counts. A peak indicates where values are most common, but doesn’t reveal their quantity. Including a short explanation in your chart caption can prevent confusion, especially for audiences less familiar with this chart type.

Examples and storytelling tips

Examples show how density plots clarify patterns and comparisons in your data. Below are practical scenarios and tips for communicating what your plot reveals.

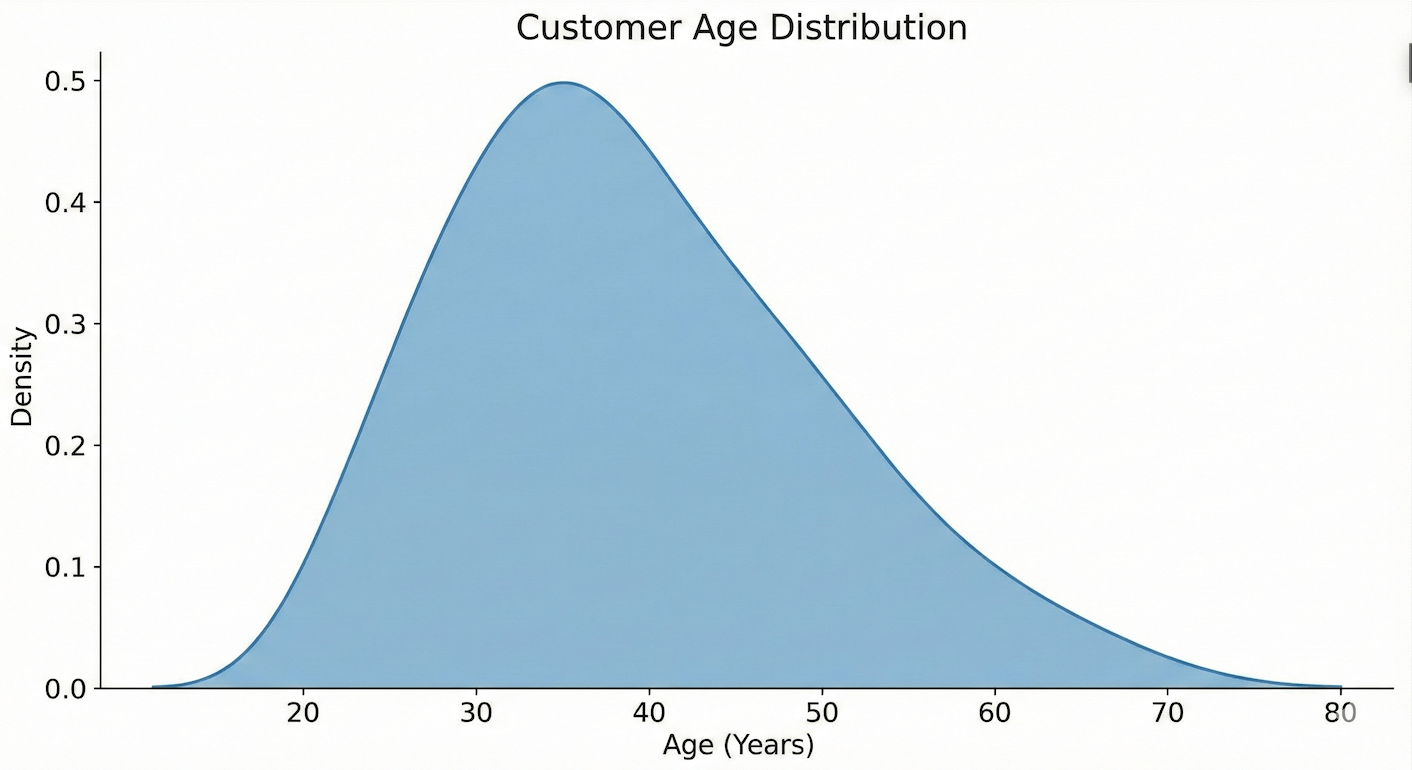
Example 1: Customer age distribution

Suppose you were to create a density plot of customer ages that revealed two peaks, one near 25 and another near 45, showing two main age groups in the customer base.

• Storytelling tip: Don’t just present the chart; interpret it. You could point to the two peaks and explain what they mean. For example: “We’ve noticed that our customers fall into two distinct age groups: a large segment of young adults in their mid-twenties and a second segment of middle-aged adults. This suggests we might actually have two different types of people we connect with.” A possible takeaway is that these two groups care about different things. This insight can directly influence marketing strategies, prompting targeted campaigns for each group.

Example 2: Response time or performance metrics

Now take the case of a software team looking at a density plot of web service response times and finding a right-skewed density plot. This could mean that most requests are fast, but a significant number take much longer.

• Storytelling tip: Focus on the shape and what it implies. For example: “We notice that most user requests are handled quickly, like the peak on the left shows. But this long tail means many of our users are still experiencing significantly slower response times. These outliers are hurting the user experience and need to be investigated.” This kind of explanation, focusing on the shape of the distribution and what it means, is far more persuasive than simply stating that the average response time is “good,” because it’s an opportunity to talk about consistency and user experience, not just averages.

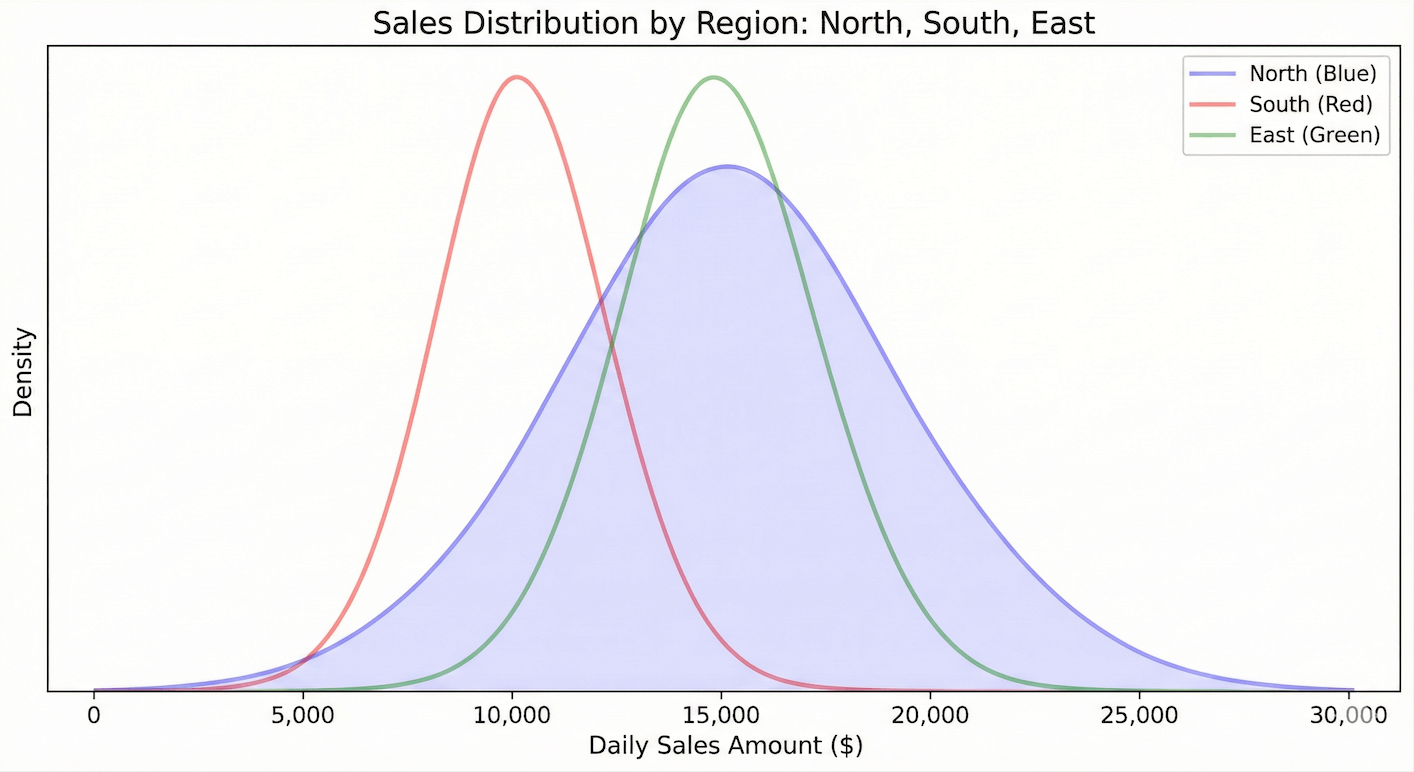
Example 3: Comparing distributions across regions

A national retail chain compares daily sales distributions across its four regions using overlapping density plots, revealing differences in peaks, spread, and overall sales performance.

• Storytelling tip: Call out the differences between the groups; describe how they differ and explain what the differences mean for the business. “As we can see, the East and West regions show similar sales distributions, with peaks around $15,000 per day. However, the South region’s distribution is shifted to the left, indicating generally lower daily sales. Meanwhile, the North region’s distribution is much wider, suggesting greater volatility in its day-to-day performance.” This comparative analysis provides actionable insights for regional managers.

General storytelling tips

• Highlight peaks and shifts: Explicitly point out where the peaks (modes) are and what they represent. If comparing plots, describe any shifts in the peaks. For example, “Group B’s peak is shifted to the right of Group A’s, indicating higher average values.”
• Call out differences in shape: Describe the spread and skewness. Is one distribution wider or narrower than another? Is one symmetric while another is skewed?
• Explain density in plain terms: When presenting to a non-technical audience, add a simple explanation. For instance, “This chart shows where the values are most clustered. Higher parts of the curve mean more data is concentrated there.”

How to create a density plot

Creating a density plot involves a few straightforward steps using most modern data analysis tools. Here is how to approach the process.

Data requirements

A density plot requires a single column of continuous, numerical data that’s clean and free of errors or non-numeric values. Data types can include metrics like sensor readings, amounts, or measurements. Avoid using density plots with missing values, text entries, or categorical data.

Steps in common tools

Here are the essential steps for creating a density plot, no matter which tool you use:

1. Prepare your data: Load your data set into your chosen tool. Isolate the column of continuous data you want to visualize. If you plan to compare distributions, you’ll also need a categorical column that you can use to group your data (e.g., a “Region” column to group sales data).
2. Apply the density or KDE (kernel density estimation) function: In your tool’s chart creation menu, look for an option named “Density Plot,” “Kernel Density Plot,” or “KDE Plot.” In some tools, like those based on programming languages (e.g., R or Python), you’ll call a specific function (like geom_density() or sns.kdeplot()). Select the numerical column as your variable.
3. Adjust smoothing and labels: Once the basic plot is generated, refine it.
   
   • Bandwidth/Smoothing: Find the setting for bandwidth (it might be called “smoothing,” “kernel width,” or similar). Experiment with different values to get a plot that’s both smooth and informative.
   • Labels: Edit the title, x-axis label, and y-axis label to be clear and descriptive. Add a legend if you are plotting multiple groups.
   • Colors and transparency: Choose a clear color scheme. If you are overlapping plots, remember to set the fill opacity to a semi transparent level.
4. Customize for context: For dashboards and reports, make sure the plot’s visual style matches the surrounding content. You might adjust fonts, remove gridlines, or add annotations to highlight key insights directly on the chart.

In Excel, since density plots aren’t built in, you can approximate one by first creating a histogram and then overlaying a smoothed line chart to mimic the density curve. This manual process is less precise than dedicated tools but gives a basic visualization when other options aren’t available.

Limitations and when to use an alternative

While density plots are powerful, they come with important limitations. It’s essential to know when another chart type might serve your needs better.

Limitations of density plots

• Can be hard to interpret: The concept of “probability density” on the y-axis isn’t intuitive for everyone. Non-technical audiences may struggle with it and misinterpret the chart as a frequency count.
• Doesn’t show exact counts: By design, a density plot smooths away individual data points and doesn’t show exact counts or frequencies. If the exact number of observations in a certain bin is important, a density plot is the wrong tool.
• Can imply data where none exists: The smoothing process can sometimes cause the curve to extend into ranges where no data exists; for example, showing a small density for negative values when all your data is positive. While usually minor, this can be misleading.

Alternatives to density plots

• Histograms: If your audience is more comfortable with concrete counts or if the exact frequency within specific bins is important, a histogram is a great alternative. It’s more straightforward to read, as the y-axis represents a simple count. The main downside is its sensitivity to bin width.
• Box plots: If you want to summarize and compare the distributions of several groups, box plots are an excellent, compact option. A box plot displays the median, quartiles, and range of the data, providing a statistical summary rather than a detailed shape. They are less cluttered than overlapping density plots when you have many groups to compare.
• Violin plots: A violin plot can be seen as a hybrid of a density plot and a box plot. It shows a density plot mirrored on both sides of a central axis, with a box plot often overlaid in the middle. This gives you the best of both worlds: a detailed view of the distribution’s shape and a summary of its key statistical properties. They are great for comparing distributions across multiple categories.

Conclusion and key takeaways

Density plots help you see distribution patterns at a glance, making it easier to spot clusters, compare groups, and understand the shape of your data beyond averages. Their smooth curves highlight where data is concentrated, providing a clear, detailed view that supports better analysis and decision-making.

To recap the most important points:

• Density plots reveal the underlying shape of data distributions by showing where values are concentrated.
• They are best used for analyzing and comparing distributions of continuous data.
• Their main advantage is the smooth representation, which avoids the binning issues of histograms.

Next time you analyze a column of numbers, look beyond the average and use a density plot to quickly uncover patterns and gain deeper insights.